Python Numeric Data Types
Handling numbers incredibly easy to understand not just how to use them, but how they work inside the computer.
Think of Python numbers like smart containers. In older languages (like C or Java), you have to pick the “size” of your container (box) before putting a number in it. If the number is too big, the box breaks (Overflow).
In Python, the boxes are made of elastic rubber; they stretch automatically to fit any number you throw at them.
–
int Integers
Think of a Python integer as a “Smart Container.” In most other languages, an integer is like a small fixed-size box (e.g., a 32-bit or 64-bit box). If you try to put a number too big for that box, it spills over (Overflow).
Python, however, uses Magic Expandable Boxes. If the number grows, the box grows with it. Whether you are storing the number 5 or the estimated number of atoms in the observable universe ($10^{80}$), Python uses the same int type to manage it all.
An integer in Python is any whole number. It can be positive, negative, or zero.
- Whole Numbers Only: An integer (
int) is any whole number without a fractional part. It can be positive, negative, or zero. - No Decimals Allowed: The moment you add a decimal point (e.g.,
10.0), Python changes the type to afloat. - Dynamic Typing: You don’t need to declare
int x = 10. Just writex = 10, and Python’s “brain” (the interpreter) figures out it’s an integer.
x = 10 # Python knows this is an int
y = -500 # Negative numbers are also ints
z = 0 # Zero is an int
print(type(x)) # Output: <class 'int'>–
From an architectural perspective, Python integers are objects, not just raw memory addresses. In the CPython implementation, even a simple integer like 0 takes up about 24 to 28 bytes of memory because it carries metadata.
- Everything is an Object: Unlike C or Java where
intis a primitive, in Python, every integer is aPyObject. This means it carries overhead:- ob_refcnt: Reference count for Garbage Collection.
- ob_type: Pointer to the integer type definition.
- ob_size: The number of “digits” (internal units) used.
- Arbitrary Precision Arithmetic: Python handles “Unlimited Precision” by storing integers as a structural array of “digits.” Instead of base-10, it typically uses base $2^{30}$. This internal complexity allows Python to handle RSA encryption keys or massive scientific calculations that would exceed the 64-bit limit of standard hardware.
- Integer Interning (Memory Optimization): To save resources, Python pre-allocates and reuses integer objects in the range of -5 to 256. When you assign
x = 100andy = 100, both variables point to the exact same memory address. This is known as Integer Interning. - The DoS Protection (Security): Because converting massive integers to strings is CPU-intensive ($O(n^2)$ complexity), Python 3.10.7+ introduced a security limit. By default, it limits string conversion to 4,300 digits to prevent Denial of Service (DoS) attacks. This can be adjusted using
sys.set_int_max_str_digits(). - Cryptography & Bit Length When dealing with encryption keys (like RSA), the number of digits doesn’t matter as much as the number of bits. Don’t convert to a string to check size; use the built-in method.
- # Python Code
x = 1 << 100 # A massive number
print(x.bit_length()) # Output: 101 (Instant and accurate)
- # Python Code
–
- Unlimited Precision –
- In languages like Java, an integer has a maximum size (e.g., up to 2 billion).
- If you go over, it crashes (Overflow Error).
- Python is different. Python integers automatically expand to use as much memory as your computer has.
- You can calculate $2^{1000}$ without any special libraries.
# This works perfectly in Python huge_number = 9999999999999999999999999999999
- Visual Separators _
- When writing code, use underscores to make large numbers readable.
- Python ignores them during execution.
salary = 10_000_000 # Same as 10000000 print(salary) # Output: 10000000
- Binary, Octal, & Hexadecimal
- Python understands more than just base-10 numbers.
- Binary (Base 2): Prefix 0b (e.g., 0b101 → 5)
- Octal (Base 8): Prefix 0o (e.g., 0o10 → 8)
- Hexadecimal (Base 16): Prefix 0x (e.g., 0xFF → 255)
- Python understands more than just base-10 numbers.
Key Components
- The
intClass: The blueprint for all whole numbers. - CPython Interpreter: The engine that manages the “elasticity” of the integer.
sysModule: The tool used to inspect memory size and security limits.
Key Characteristics
- Immutable: Once an integer object is created in memory, it cannot be changed. If you do
x = x + 1, Python creates a new object for the result. - Unlimited Size: Limited only by your computer’s physical RAM.
- Multiple Representations: Supports Binary, Octal, and Hexadecimal.
Use Cases
- Security & Cryptography: Generating 2048-bit or 4096-bit keys for SSL/TLS.
- Financial Tech: Precise counting of transactions (where floats might cause rounding errors).
- Scientific Computing: Calculating factorial of 1000 or astronomical distances.
Benefits
- Safety: No “Integer Overflow” bugs that lead to security vulnerabilities.
- Readability: Support for underscores (e.g.,
1_000_000) makes code easier to audit. - Flexibility: Easily convert between different number bases (Hex to Dec).
Technical Challenges
- Memory Usage: Storing millions of small integers can consume significantly more RAM than a C-array of 32-bit ints.
- Speed: Performing math on “Magic Boxes” is slightly slower than “Fixed Boxes” because Python has to check the size of the box before every calculation.
Limitations & Security (DoS Protection)
- Converting a massive integer to a string (like printing a number with 1 million digits) is very CPU-heavy. To prevent Denial of Service (DoS) attacks where an attacker forces a server to spend hours calculating a string, Python 3.10.7+ introduced a limit:
- Default Limit: 4,300 digits for string conversion.
Common Problems and Solutions
| Problem | Symptom | Solution |
| ValueError | “Exceeds the limit (4300) for integer string conversion” | Use sys.set_int_max_str_digits(0) to remove the limit (use with caution). |
| High Memory Usage | RAM fills up when storing long lists of numbers. | Use the NumPy library or array module for fixed-size C-style integers. |
| Type Confusion | 10 / 2 results in 5.0 (float) instead of 5. | Use Floor Division 10 // 2 to keep the result as an int. |
Cheat Sheet
| Feature | Syntax / Example | Notes |
| Check Type | type(10) | Returns <class 'int'> |
| Binary | 0b1010 | Binary for 10 |
| Hexadecimal | 0xA | Hex for 10 |
| Readability | 1_000_000 | Underscores are ignored by Python |
| Large Numbers | 10**100 | Google (1 followed by 100 zeros) |
| Conversion | int("10") | Converts a string to an integer |
- Boolean Subclass: Did you know
bool(True/False) is actually a “child” ofint?Truebehaves like1andFalselike0. TryTrue + 1it equals2! - Bitwise Operations: Because integers are stored in binary internally, Python is incredibly fast at bitwise ops (
&,|,^,<<,>>), which are essential for DevSecOps tasks like IP address masking and firewall rule logic.
Built-in Types , Integer Objects
Lab Python Integer
Quiz Python Integer
float : Floating Point Numbers
float : Floating Point Numbers Used to represent decimal values. Think of a float as a measuring tape or scientific notation ($1.5 \times 10^2$). While Integers count whole items (1 user, 2 servers), Floats measure continuous data like server latency (12.5ms) or transaction amounts ($19.99).
Think of a float as a scientific notation on a calculator. This allows the computer to store very large or very small numbers using a fixed amount of memory.
- Definition: Any number with a decimal point is a float in Python (e.g.,
10.5,3.0,-0.01). - Scientific Notation: You can use
eorEto represent powers of 10. For example,2e3is 2×103, which equals2000.0. - Dynamic Typing: Python automatically treats any division result as a float. Even
4 / 2results in2.0. - Type Conversion: You can turn an integer or a string into a float using the
float()function.
In Python, you don’t need to tell the computer “this is a float.” It automatically understands:
- Decimal presence:
price = 19.99(Float) - The “.0” rule:
val = 5.0is a float, even though it’s a whole number. - Positive & Negative:
temp = -10.5is perfectly valid.
price = 19.99
pi = 3.14159
val = 1.0 # Even with .0, this is a floatScientific Notation (The ‘e’ notation)
When numbers get extremely large (like the distance to stars) or tiny (like the size of an atom), we use e.
a = 1.5e2→ 1.5×102=150.0b = 3e-4→ 3×10−4=0.0003c = 2.5e6→ 2,500,000.0
–
Computers store numbers in binary (0s and 1s). Some simple decimals (like 0.1) translate to infinite repeating fractions in binary. Because memory is limited, the computer chops off the end, leading to tiny errors.
The “0.1 + 0.2” Problem:
val = 0.1 + 0.2
print(val)
# Output is NOT 0.3
# Output: 0.30000000000000004
NEVER compare floats using ==.
- if 0.1 + 0.2 == 0.3: (This will fail)
- if abs((0.1 + 0.2) – 0.3) < 0.00001: (Check if they are “close enough”)
At an architect, you must understand that Python floats follow the IEEE 754 double-precision binary floating-point standard.
Precision Limits: A float is stored in 64 bits: 1 bit for the sign, 11 bits for the exponent, and 52 bits for the fraction (mantissa). This provides roughly 15–17 decimal digits of precision.
| Feature | Specification | Impact on Coding |
| Total Bits | 64 bits | Determines the fixed memory footprint of every float. |
| Sign Bit | 1 bit | Allows for signed zeros (both 0.0 and -0.0 exist). |
| Exponent | 11 bits | Dictates the range (approx. $10^{-308}$ to $10^{308}$). |
| Mantissa | 52 bits | Limits precision to roughly 15–17 decimal digits. |
| Implicit Bit | 1 bit | Gives an effective 53 bits of precision for normalized numbers. |
| Comparison | math.isclose() | Never use == due to bit-level representation errors. |
The Binary Representation Trap: Machines speak binary (0s and 1s). Some decimal fractions (like 0.1) cannot be represented exactly in binary. This leads to the famous 0.1 + 0.2 != 0.3 issue.
Special Values:
float('inf'): Infinity (larger than any other number).float('-inf'): Negative Infinity.float('nan'): “Not a Number” (used for undefined calculations like0 / 0in some libraries or missing data in Pandas).
Security Implication: In financial DevSecOps, never use floats for currency. Use the Decimal module to avoid rounding errors that could lead to “salami slicing” fraud or balance mismatches.
- Float Injection – The
NaNAttack When accepting JSON input in an API, standard JSON does not supportNaN(Not a Number) orInfinity. However, some Python parsers might accept them if configured loosely.- Risk: If an attacker injects
NaNinto a financial calculation, it can corrupt the entire mathematical pipeline (because5 + NaN = NaN). - Defense: Always validate input using
math.isnan()before processing metrics.
- Risk: If an attacker injects
–
Key Components & Characteristics
| Component | Description |
| Significand (Mantissa) | The actual digits of the number. |
| Exponent | Determines where the decimal point “floats”. |
| Imprecision | The inherent “approximation” in binary decimals. |
| Epsilon | The smallest difference between two distinct floats. |
Use Cases & Benefits
- Data Science: Handling weights in neural networks using NumPy.
- Physics Simulations: Calculating trajectories or fluid dynamics.
- Geo-location: Storing Latitude and Longitude coordinates.
- Performance: Floats are handled directly by the CPU’s Floating Point Unit (FPU), making them much faster than the
Decimalclass for bulk calculations.
Technical Challenges & Common Issues
- Rounding Errors
- Problem:
0.1 + 0.1 + 0.1might result in0.30000000000000004. Solution: Useround(value, digits)for display ormath.isclose()for comparisons.
- Problem:
- Equality Testing
- Problem:
if x == 0.3:will often fail due to precision issues. Solution: Use a “tolerance” (epsilon) approach.
- Problem:
import math
if math.isclose(a, b, rel_tol=1e-9):
# This is the safe way to compare floats
Cheat Sheet
| Task | Code Snippet |
| Convert to Float | float("10.5") |
| Check if NaN | math.isnan(x) |
| Infinity | float('inf') |
| Power of 10 | 1e-3 (equals 0.001) |
| Safe Comparison | math.isclose(a, b) |
Lab Python float
Quiz Python float
complex : Python Complex Numbers
In Python, complex numbers are a built-in numeric type used to represent numbers with both a real and an imaginary part. While they might seem intimidating, they are essential for signal processing, electrical engineering, and advanced mathematical simulations.
Think of a complex number as a coordinate on a 2D map. A regular number (integer or float) only moves you left or right on a single line. A complex number adds a second dimension (up and down), allowing you to describe any point on a flat surface using two values: the Real part and the Imaginary part.
Think of a complex number as a Vector in a 2D game. The real part is your horizontal position (x), and the imaginary part is your vertical position (y). To handle both simultaneously, Python packages them into a single object.
- Syntax: In Python, the imaginary part is denoted by the suffix
jorJ(not i, as used in traditional mathematics).- Example:
z = 3 + 4j
- Example:
- The
complex()Constructor: You can create them usingcomplex(real, imag).- Example:
complex(2, 5)results in(2+5j).
- Example:
- Accessing Parts: Every complex object has
.realand.imagattributes.z = 5 + 2jz.realreturns5.0z.imagreturns2.0
- Automatic Casting: If you add an integer to a complex number, the result is always complex.
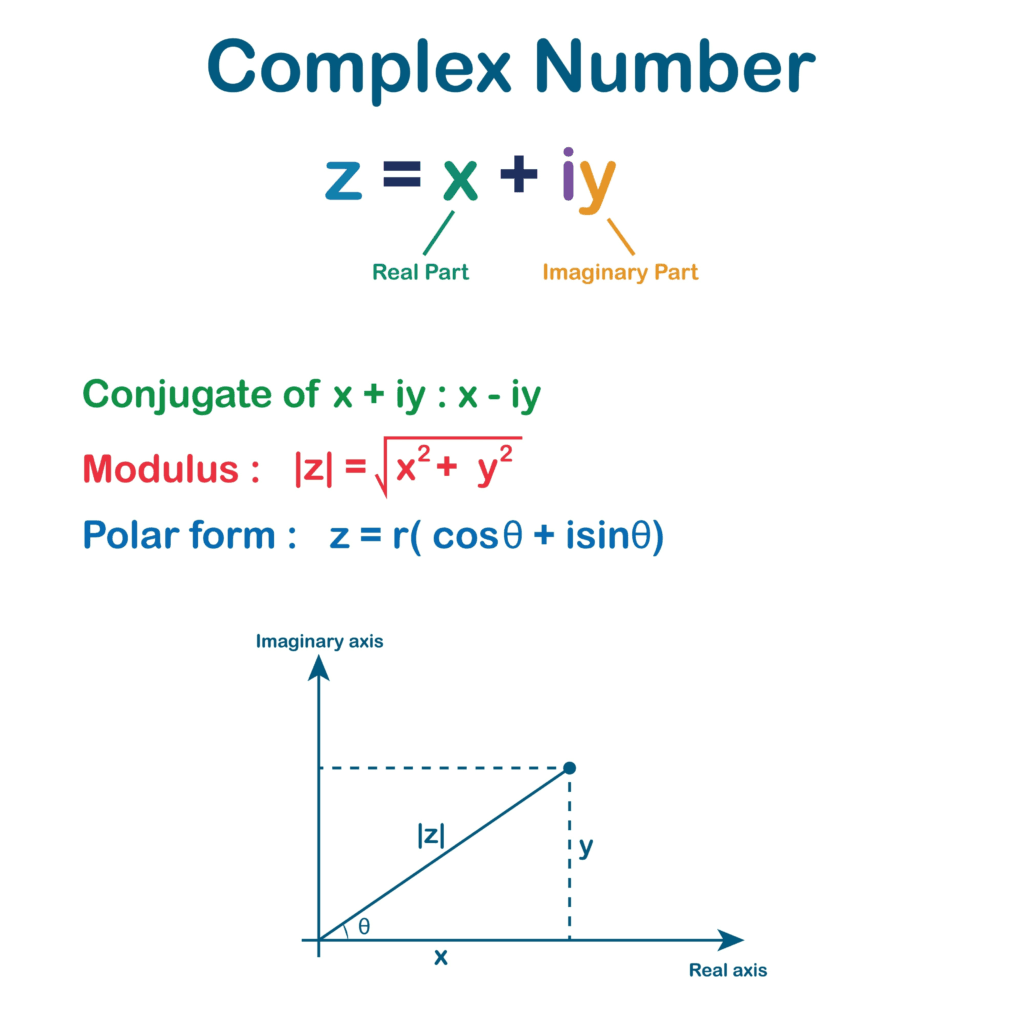
–
Architecting systems for scientific computing or cryptography requires understanding the underlying implementation of the complex type.
- Memory Layout: A Python complex number is a wrapper around two C-style
double(float64) values. It occupies 32 bytes (compared to 24 bytes for a float), making it memory-intensive for massive arrays. - Phase and Magnitude:
- The
cmathModule: For complex numbers, the standardmathmodule won’t work. You must use the cmath (Complex Math) library for square roots, logarithms, and trigonometric functions of complex numbers. - Immutability: Like integers and floats, complex numbers are immutable. Any operation creates a new object in memory.
–
Key Components & Characteristics
| Component | Description | Python Attribute |
| Real Part | The standard number part. | z.real |
| Imaginary Part | The part multiplied | z.imag |
| Conjugate | The number with the sign of the imaginary part flipped. | z.conjugate() |
| Magnitude | The distance from the origin | abs(z) |
–
Use Cases & Benefits
- Electrical Engineering: Representing Impedance and Alternating Current (AC).
- Signal Processing: Fast Fourier Transforms (FFT) used in audio and video compression via SciPy.
- Quantum Computing: State vectors in quantum simulations are complex.
- Control Systems: Analyzing the stability of automated systems in DevSecOps pipelines.
Technical Challenges & Common Issues
- The “j” Suffix Requirement
- Problem: Writing
z = 3 + jresults in aNameErrorbecause Python thinksjis a variable. Solution: Always use a literal number before thej. Writez = 3 + 1j.
- Problem: Writing
- Comparison Limitations
- Problem: You cannot use comparison operators like
<or>with complex numbers. Reason: Complex numbers do not have a natural ordering on a 2D plane. Solution: Compare their magnitudes instead:abs(z1) > abs(z2).
- Problem: You cannot use comparison operators like
Cheat Sheet
| Task | Syntax | Result Example |
| Creation | complex(3, 2) | (3+2j) |
| Get Real Part | z.real | 3.0 |
| Get Imaginary | z.imag | 2.0 |
| Complex Conjugate | z.conjugate() | (3-2j) |
| Magnitude | abs(z) | 3.605... |
| Square Root | cmath.sqrt(z) | Returns a complex root |
Lab Python complex
Quiz Python complex
bool : Booleans
The Boolean data type (bool) is the simplest yet most powerful tool. It represents the truth value of an expression. booleans are the “gatekeepers” that decide if a build passes, if a user is authenticated, or if a security group is open.
Think of a Boolean as a Light Switch. It has only two possible states: ON (True) or OFF (False). Every decision a computer makes is eventually boiled down to a series of these True/False switches.
Think of a boolean as a binary gate in a circuit. If the electricity flows, the result is True (1). If the circuit is broken, the result is False (0).
- The Two Values: Python has two boolean keywords:
TrueandFalse.- Note: They are case-sensitive.
trueorFALSEwill result in aNameError.
- Note: They are case-sensitive.
- Comparison Operators: These are symbols that return a boolean value:
==(Equal to)!=(Not equal to)>(Greater than)<(Less than)
- Logical Operators: Used to combine boolean values:
and: ReturnsTrueonly if both are True.or: ReturnsTrueif at least one is True.not: Flips the value (not TruebecomesFalse).
–
At an architect level, you must understand how Python handles Booleans under the hood to write highly optimized and secure code.
- Booleans are Integers: In Python,
boolis a subclass ofint.Trueis actually1.Falseis actually0.- You can technically perform math with them:
True + Trueequals2. (Though you should avoid this for code clarity).
- The “Truthy” and “Falsy” Concept: Every object in Python has a boolean value. You can check this using the
bool()function.- Falsy values:
None,False,0,0.0,0j,""(empty string),[](empty list),{}(empty dict). - Truthy values: Everything else.
- Falsy values:
- Short-Circuit Evaluation: Python evaluates logical expressions from left to right and stops as soon as the result is certain.
- In
A or B, ifAisTrue, Python doesn’t even look atB. - DevSecOps Tip: Use this to prevent errors. Example:
if list and list[0] == 'admin':. If the list is empty, the second part never runs, preventing anIndexError.
- In
- Identity vs. Equality: *
==checks if values are the same.ischecks if they are the exact same object in memory.- Always use
if is_valid:orif is_valid is True:, though the former is preferred.
You can mathematically add them (though you shouldn’t, for code clarity):
print(True + True) # Output: 2
print(False * 100) # Output: 0The Power of “Truthy” & “Falsy” (The Invisible Booleans)
In Python, you don’t always need to type True or False. Python evaluates the “truthfulness” of every object. This allows for cleaner, more “Pythonic” code.
| Data Type | “Falsy” Values (Evaluates to False) | “Truthy” Values (Evaluates to True) |
| Numbers | 0, 0.0, 0j | Any non-zero number (1, -5, 0.001) |
| Strings | "" (Empty String) | Any string with characters (" ", "0", "False") |
| Collections | [], {}, (), set() | Any non-empty collection |
| Constants | None, False | True |
# Practical Example
username = ""
if username:
print(f"Welcome {username}")
else:
print("Username is empty!") # This runs because "" is FalsyAdvanced Boolean Logic: De Morgan’s Laws
When you have complex not, and, and or statements, code becomes hard to read. De Morgan’s Laws help you simplify them.
- Rule 1:
not (A and B)is the same as(not A) or (not B) - Rule 2:
not (A or B)is the same as(not A) and (not B)
Example: Imagine you want to check if a user is invalid.
- Hard to read:
if not (user.is_active and user.has_permission): - Simplified:
if (not user.is_active) or (not user.has_permission):
The Ternary Operator (One-Line Logic)
Masters don’t write 4 lines of code when 1 will do. The Ternary Operator allows you to assign values based on a condition in a single line.
Syntax: value_if_true if condition else value_if_false
Example:
# Beginner Way
if score > 50:
status = "Pass"
else:
status = "Fail"
# Master Way (Ternary)
status = "Pass" if score > 50 else "Fail"Key Components & Characteristics
| Component | Description |
| Keywords | True, False. |
| Function | bool(x) – converts any value to a boolean. |
| Logic Gates | and, or, not. |
| Short-Circuit | Optimization where evaluation stops early. |
Use Case & Benefits
- Conditional Branching: Using
ifstatements to control program flow. - Loop Control: Using a boolean flag to start/stop a
whileloop. - Security Validation: Checking
is_authenticatedorhas_permission. - Feature Flags: Enabling or disabling features in production without redeploying code.
Technical Challenges & Common Issues
| Challenge | Explanation | Solution |
True == 1 | True acts like the integer 1 in math. True + True is 2. | Avoid doing math with booleans unless doing code golf. |
bool("False") | The string “False” is not empty, so it is True. | Always compare strings: val == "False". |
is vs == | True is 1 is False. True == 1 is True. | Use if variable: for checking boolean truth, not == True. |
1. Confusion with Strings
Problem: bool("False") returns True. Why? Because "False" is a non-empty string, and all non-empty strings are “Truthy.” Solution: Explicitly compare strings: input_val.lower() == "true".
2. The is vs == Pitfall
Problem: 1 == True is True, but 1 is True is False. Why? == compares the value (1 vs 1), but is checks the object type (Integer vs Boolean).
Cheat Sheet
| Expression | Result | Why? |
bool(0) | False | Zero is always falsy. |
bool(" ") | True | A string with a space is NOT empty. |
True and False | False | and requires both to be True. |
False or True | True | or only requires one to be True. |
not False | True | Inverse of False. |
Lab Python bool
Quiz Python bool
none : NoneType
None is a special constant that represents the absence of a value or a null state. It is not zero, it is not false, and it is not an empty string. It is a datatype of its own called NoneType.
None is critical for avoiding the dreaded AttributeError: 'NoneType' object has no attribute... which crashes pipelines and scripts daily.
Think of None as a placeholder in a database form. If a user doesn’t enter a middle name, the database stores NULL (which maps to None in Python), not the string “Null”.
None is a special data type called NoneType. It represents null, void, or nothingness.
- It is not 0.
- It is not False.
- It is not an empty string “”.
- It is simply… nothing.
- The Keyword:
None(Case sensitive). - The Type: It is the only value of the type
NoneType. - Implicit Returns: If a function doesn’t explicitly
returna value, Python automatically returnsNone. - Printing:
print(None)outputsNone. - Logic:
Noneis considered “Falsy” (evaluates toFalsein anifstatement).
At the architect level, you must treat None as a Singleton. This means there is only one None object in the entire Python program’s memory.
- The Singleton Pattern:
- Every time you assign
x = None, you are pointing to the exact same memory address. - Memory Efficiency: Since it’s a singleton, checking for
Noneis extremely fast.
- Every time you assign
- The “Sentinel” Usage:
Noneis often used as a default value for function arguments to signal “Use the standard behavior.”
- The
isvs==Rule (Crucial):- Rule: Always use
if x is None:. Never useif x == None:. - Reason: A custom class can override the
__eq__(equality) method to returnTrueeven if it isn’tNone. Theisoperator ignores overrides and checks memory identity directly.
- Rule: Always use
- Type Hinting:
- In modern Python (DevSecOps scripts), use type hints to indicate a value can be
None. def connect(url: str) -> Optional[int]:(Requiresfrom typing import Optional).
- In modern Python (DevSecOps scripts), use type hints to indicate a value can be
Key Components & Characteristics
| Component | Description |
| Truthiness | bool(None) is always False. |
| Comparisons | Not ordered. None > 0 raises a TypeError. |
| Memory | Singleton (Fixed memory address). |
| Safety | Accessing attributes/methods on None causes a crash. |
Use Cases & Benefits
- Variable Initialization:
result = None(waiting for data). - Error Handling: A function returns
Noneto indicate failure without throwing an exception (e.g.,dict.get('missing_key')returnsNone). - Optional Arguments: Allowing users to skip parameters in CLI tools.
Technical Challenges & Common Issues
1. The Comparison Trap (== vs is)
Problem: A custom class can override the __eq__ method to return True when compared to None, creating logic bugs. Solution: Always use is None or is not None.
# BAD
if x == None:
pass
# GOOD (Architect Standard)
if x is None:
pass
2. Attribute Error Loop
Problem: Trying to access a method on a variable that unexpectedly became None. Error: AttributeError: 'NoneType' object has no attribute 'lower'. Solution: Always guard your calls.
name = None
# print(name.lower()) # CRASH!
if name:
print(name.lower()) # Safe
Cheat Sheet
| Task | Code Snippet | Why? |
| Check for None | if x is None: | Faster and safer than ==. |
| Check if NOT None | if x is not None: | Standard “Guard clause”. |
| Assign Default if None | x = val or "default" | Uses Falsy logic (careful if val is 0). |
| Safe Dictionary Get | data.get('key') | Returns None instead of crashing. |
Lab Python NoneType
Quiz Python NoneType
Type Casting (Conversion)
You are travelling from India to the USA. In India, you use Rupees (INR). But in the USA, you cannot use Rupees directly; you must convert them into Dollars (USD) to buy coffee or a taxi ticket.
Type Casting is exactly like this currency exchange.
- Data in Python comes in different “currencies” or types (like Integers, Strings, Floats).
- Sometimes, Python automatically changes the currency for you (Implicit Casting).
- Other times, you must go to the exchange counter and manually change it yourself (Explicit Casting).
If you try to add a Name (String) to a Number (Integer), Python gets confused just like a shopkeeper would if you tried to pay in Rupees in New York! Type casting fixes this confusion.
Type Casting is simply converting one data type into another.
1. Implicit Type Casting (Automatic)
Python is smart. If you add an integer (whole number) and a float (decimal number), Python automatically converts the answer to a float so you don’t lose the decimal part. You don’t have to do anything!
- Example:
10 (int) + 2.5 (float) = 12.5 (float)
2. Explicit Type Casting (Manual)
This is where you force Python to convert data. We use special “Constructor Functions” for this.
int(): Converts to Integer.int("10")->10
float(): Converts to Float.float("10.5")->10.5
str(): Converts to String.str(20)->"20"
–
1. Loss of Data (Narrowing Conversion)
When you convert a float to an int, Python simply cuts off the decimal part. It does not round up; it just chops it off.
int(9.99)becomes9, not10. This is critical for financial calculations!
2. The String Trap
You cannot convert a non-number string directly to an integer.
int("Hello")-> Error! (ValueError)int("10.5")-> Error! (ValueError). You must doint(float("10.5")).
3. Collection Casting
You can convert lists to tuples or sets easily. This is a pro trick to remove duplicates!
my_list = [1, 2, 2, 3]set(my_list)->{1, 2, 3}(Duplicates removed instantly!)
4. Byte Order (Endianness):
The Network Engineer’s Nightmare When casting Integers to Bytes for network packets, you must specify the order: Big Endian (standard for networks) or Little Endian (standard for Intel CPUs). If you get this wrong, the firewall will read the packet header backwards.
port = 8080
# Convert to bytes for network transmission (Big Endian)
packet_data = port.to_bytes(2, byteorder='big')–
As a DevSecOps Architect, you are not just writing simple scripts. You are building automation pipelines, security tools, and handling network traffic. Type casting here is about Security, Protocol Compatibility, and Data Integrity.
Environment Variable Handling (The os Module)
When you read configurations from your server (using os.environ), everything comes as a String. Even if you set PORT=8080, Python reads it as "8080".
- Architect Challenge: Passing
"8080"to a socket connection will crash your app. - Solution: You must cast environment variables immediately.
import os
port = int(os.getenv("PORT", 8080)) # Safe casting with default
debug_mode = bool(os.getenv("DEBUG", "False")) # Watch out! bool("False") is True.- Note:
bool("False")returnsTruebecause the string is not empty. You need logic:os.getenv("DEBUG") == "True".
Network Socket Programming (Bytes vs. Strings)
In DevSecOps, we deal with raw network packets. Python 3 strictly separates Strings (Unicode) and Bytes.
- Scenario: You cannot send a String
"GET / HTTP/1.1"over a network socket. - Casting: You must Encode (Str -> Bytes) and Decode (Bytes -> Str).
message = "Hello Server"
byte_data = message.encode('utf-8') # Cast to bytes
# Send byte_data over socket...JSON Serialization & Security Parsing
Security tools often output JSON. When parsing logs (e.g., from AWS CloudWatch), timestamps come as strings.
- Architect Task: Convert String Timestamp -> Datetime Object for time-based logic (e.g., “Block IP if attack happened < 5 mins ago”).
from datetime import datetime
log_time = "2023-10-27T10:00:00"
real_time = datetime.fromisoformat(log_time) # Advanced Type Casting- Custom Class Casting: You can teach your own Python objects how to behave like integers or strings by defining “Magic Methods” like
__int__or__str__inside your class. - Safe Casting: Always wrap casting in a
try...exceptblock in production code. If a user enters “ten” instead of “10”, your whole security pipeline shouldn’t crash!
- Pydantic (Data Validation): Official Pydantic Docs – Automatically casts and validates types for APIs.
- Scapy (Packet Manipulation): Official Scapy Docs – heavily relies on casting bytes for custom packet crafting.
- Click (CLI Creation): Official Click Docs – Handles command-line argument type casting automatically.
Key Components Overview
| Component | Description |
| Implicit Casting | Automatic conversion by Python (e.g., Int to Float). Risk-free but limited. |
| Explicit Casting | Manual conversion using int(), str(), etc. Powerful but risky (can error). |
| Encoding/Decoding | Specific casting between Text (Str) and Binary (Bytes). Critical for Networking. |
| Serialization | Converting complex objects (Dicts, Lists) to Strings (JSON) for storage. |
Key Characteristics
- Dynamic: Python figures out types at runtime, but casting forces a specific type.
- Strongly Typed: Python will NOT let you add “5” + 5 implicitly (unlike JavaScript). You must cast.
Use Cases
- User Input:
input()always returns a string. Must cast tointfor calculations. - API Development: converting database rows (Tuples) into JSON (Strings).
- Cryptography: converting passwords (Strings) to Bytes for hashing algorithms.
Benefits
- Data Integrity: Ensures math is done on numbers, not text.
- Memory Optimization: Storing data as bytes or tuples is often smaller than strings or lists.
- Flexibility: Allows different systems (Database vs. Frontend) to talk to each other.
Technical Challenges
- Precision Loss: Converting
floattointloses data. - Unicode Errors: Converting bad bytes to strings can cause
UnicodeDecodeError. - Runtime Crashes:
int("abc")crashes the program if not handled.
imitations
- You cannot cast everything to everything. You cannot cast a complex dictionary structure directly to a simple integer.
- Casting takes CPU time. Excessive casting in a high-speed loop (like packet sniffing) can slow down performance.
Common Issues, Problems & Solutions
| Common Issue | Why it happens? | Solution |
ValueError: invalid literal for int() | Trying to cast a non-number string (e.g., “xyz”) to int. | Use try-except block or validate input with .isdigit(). |
TypeError: can only concatenate str... | Adding a String and an Integer. | Cast the integer to string: str(number). |
AttributeError | Treating an Integer like a String (e.g., trying to use .upper() on a number). | Ensure variable is cast to str before string operations. |
| Decimal Truncation | int(5.9) becomes 5. | Use round(5.9) before casting if you want the nearest whole number. |
Cheat Sheet
| Function | Converts To | Example Input | Result | Note |
int() | Integer | "5" | 5 | Removes decimals if input is float. |
float() | Decimal | 5 | 5.0 | Adds precision. |
str() | Text | 100 | "100" | Safe for almost anything. |
bool() | Boolean | 0 or "" | False | Empty/Zero is False; everything else is True. |
list() | List | (1,2) | [1,2] | Makes it mutable (changeable). |
tuple() | Tuple | [1,2] | (1,2) | Makes it immutable (read-only). |
set() | Set | [1,2,2] | {1,2} | Removes duplicates. |
hex() | Hexadecimal | 255 | "0xff" | Used in memory/color coding. |
bytes() | Bytes | [65] | b'A' | Used in raw data handling. |
- Python 3 Standard Types: https://docs.python.org/3/library/stdtypes.html
- Python ‘typing’ Module (For Hinting): https://docs.python.org/3/library/typing.html
Lab Python Type Casting
Quiz Python Type Casting
Mathematical Functions
Think of Python’s math capabilities like a scientific calculator built directly into your programming language, but infinitely more powerful. You don’t need to manually calculate square roots or logarithms; you just ask Python to do it for you.
For most standard tasks, Python comes with a built-in library called math. You don’t need to install anything; just import it and start calculating.
Imagine the math module is a toolbox. You don’t carry every tool (hammer, saw, drill) in your pocket all the time because it would be heavy (slow). When you need to do specific work (math), you open the toolbox (import math) and pick the specific tool you need (e.g., math.sqrt()).
Basic Arithmetic & Number Theory
These functions help you handle integers and floating-point numbers cleanly.
| Function | Description | Example | Output |
math.ceil(x) | Rounds a number UP to the nearest integer. | math.ceil(4.2) | 5 |
math.floor(x) | Rounds a number DOWN to the nearest integer. | math.floor(4.9) | 4 |
math.fabs(x) | Returns the absolute (positive) value. | math.fabs(-7.5) | 7.5 |
math.factorial(x) | Returns $x!$ (x factorial). | math.factorial(5) | 120 |
math.gcd(a, b) | Greatest Common Divisor of a and b. | math.gcd(12, 18) | 6 |
Power & Logarithmic Functions
Essential for scientific calculations and algorithms scaling.
math.pow(x, y): Returns x raised to the power of y (xy).- Note:
math.pow(2, 3)returns8.0(float), while2**3returns8(int).
- Note:
math.sqrt(x): Returns the square root of x (x).
math.log(x): Returns the natural logarithm (base e).math.log10(x): Returns the base-10 logarithm.
Trigonometry
Python uses radians for trigonometric functions, not degrees. This is a common point of confusion!
- Conversion:
math.degrees(x): Converts radians to degrees.math.radians(x): Converts degrees to radians.
- Functions:
math.sin(x),math.cos(x),math.tan(x).
–
When you step into data science, engineering, or signal processing, the basic math module might not be enough.
The cmath Module (Complex Math)
Standard math functions fail if you try to find the square root of a negative number. In advanced mathematics, this is valid and results in a Complex Number.
- Use Case: Electrical engineering (AC circuits), signal analysis.
- How to use:
import cmath
import cmath
# Square root of a negative number
print(cmath.sqrt(-1))
# Output: 1j (where 'j' is the imaginary unit)NumPy (Numerical Python)
This is the heavy lifter. If you need to perform a math operation on 1 million numbers at once, standard Python lists are too slow. NumPy is optimized for speed.
- Key Feature: Vectorization (doing math on entire arrays without loops).
- Analogy: Standard Python is like a chef chopping vegetables one by one. NumPy is an industrial food processor that chops 100 vegetables instantly.
import numpy as np
# Create an array of data
data = np.array([1, 4, 9, 16, 25])
# Calculate square root of ALL numbers at once
print(np.sqrt(data))
# Output: [1. 2. 3. 4. 5.]
–
As a DevSecOps Architect, you aren’t just calculating numbers; you are using math to secure infrastructure and optimize cloud costs.
Cryptography & Randomness
Never use the standard random module or math functions for generating secrets, passwords, or keys. They are “pseudo-random” and predictable by hackers.
- The Architect’s Tool:
secretsmodule. - Why: It uses the OS’s true entropy source.
import secrets
# Generate a secure token for a password reset link
secure_token = secrets.token_hex(16)
print(secure_token)Capacity Planning (Linear Regression)
Use mathematical functions to predict when your server disk will get full based on past growth rates. You can write a simple script using scipy or numpy to fit a line to your monitoring data (Prometheus metrics) and alert before a crash happens.
Floating Point Precision (The Money Problem)
Architect Warning: Never use standard float for financial calculations (money).
- The Issue: Computers store floats in binary.
0.1 + 0.2in Python is often0.30000000000000004. - The Solution: Use the
decimalmodule for exact precision.
from decimal import Decimal
price = Decimal('0.1')
tax = Decimal('0.2')
total = price + tax
print(total) # Output: 0.3 (Exact!)Key Components
- Constants:
math.pi(3.14159…),math.e(Euler’s number). - Arithmetic: Factorials, GCD, Remainders.
- Transcendental Functions: Logarithms, Exponentials, Trigonometry.
- Special Functions: Gamma functions (
math.gamma), Error functions (math.erf).
Key Characteristics
- Precision: Standard floats have about 15-17 decimal digits of precision.
- Performance: Built-in modules are written in C, making them very fast.
- Immutability: Math functions return new values; they do not change the input variables.
Cheat Sheet
| Category | Function | Code Example | Result |
| Constants | Pi ($\pi$) | math.pi | 3.1415... |
| Rounding | Ceiling | math.ceil(4.1) | 5 |
| Floor | math.floor(4.9) | 4 | |
| Truncate | math.trunc(4.9) | 4 | |
| Roots/Power | Square Root | math.sqrt(16) | 4.0 |
| Power | math.pow(2, 5) | 32.0 | |
| Logarithms | Log (Base e) | math.log(10) | 2.302... |
| Log (Base 10) | math.log10(100) | 2.0 | |
| Trig | Sine | math.sin(math.radians(30)) | 0.5 |
| Advanced | Combinations | math.comb(5, 2) | 10 |
Challenges, Limitations & Common Issues
| Issue | Description | Solution |
| Domain Errors | Trying math.sqrt(-1) or math.log(0). | Check inputs before calculation or use try-except blocks. Use cmath for negative roots. |
| Rounding Errors | Floating point inaccuracy (0.1 + 0.2 != 0.3). | Use math.isclose(a, b) for comparison instead of ==. Use decimal for money. |
| OverflowError | Result is too large for Python to handle (e.g., math.pow(10, 1000)). | Use try-except OverflowError. For large integers, Python handles them automatically, but floats have limits. |
| Degrees vs Radians | Passing degrees directly to math.sin(). | Always wrap degrees in math.radians(). |